Question

Based on this data, are "being in high school" and "GPA above 3.0" independent events? Yes, P(high school ∩ GPA above 3.0) = P(high school) ⋅ P(GPA above 3.0) No, P(high school ∩ GPA above 3.0) = P(high school) ⋅ P(GPA above 3.0) Yes, P(high school ∩ GPA above 3.0) ≠ P(high school) ⋅ P(GPA above 3.0) No, P(high school ∩ GPA above 3.0) ≠ P(high school) ⋅ P(GPA above 3.0)

Answer 1

No, P(high school | GPA above 3.0) ≠ P(high school)

Explanation:

Given

See attachment for table

Required

Determine if High school and GPA above 3.0 are independent

Let

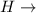`H \to` High school

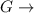`G \to` GPA above 3.0

For both events to be independent, the following must be true

`P(H\ |\ G) = P(H)`

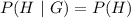
From the table:

`P(H) = (H)/(Total)`

`P(H) = (60)/(100) = 0.60`

`P(H | G) = (H\ n\ G)/(G)`

`P(H | G) = (14)/(40) = 0.35`

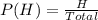
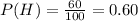
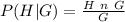
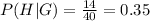
The test for independence is as follows:

`P(H\ |\ G) = P(H)`

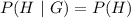
By comparison

`P(H\ |\ G) \\e P(H)`

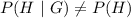
i.e.

`0.35 \\e 0.60`

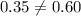
Hence, both events are not independent