Question

For what value of k are the roots of the quadratic

equation kx²+ 4x+ 1=0 equals and reals."
​

Answer 1

k ≥ 4

Explanation:

A Quadratic equation is given to us and we need to find out the value of k for which the equation has real roots. The given equation is ,

`\rm\implies kx^2 +4x +1=0`

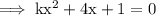
With respect to Standard form of Quadratic equation :-

`\rm\implies ax^+bx+c=0`

For real roots ,

`\rm\implies Discriminant = b^2-4ac\geq 0`

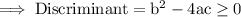
Substitute the respective values ,

`\rm\implies b^2-4ac \geq 0\\`

`\rm\implies 4^2 - 4(k)(1) \geq 0 \\`

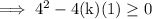
Simplify the LHS ,

`\rm\implies 16 - 4k \geq 0 \\`

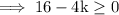
Add 4k both sides ,

`\rm\implies 4k\geq 16`

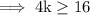
Divide both sides by 4 ,

`\rm\implies \boxed{\blue{\rm k \geq 4}}`