Question

Find the coordinates of the point on the curve

y = (2x - 3)2 at which the gradient of the
tangent is 4.​

Answer 1

(2, 1 )

Explanation:

Using differential calculus

Given

y = (2x - 3)² = 4x² - 12x + 9 , then

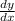`(dy)/(dx)` = 8x - 12

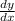`(dy)/(dx)` is the measure of the gradient of the tangent , thus equate to 4

8x - 12 = 4 ( add 12 to both sides )

8x = 16 ( divide both sides by 8 )

x = 2

Substitute x = 2 into the equation for corresponding y- coordinate

y = (4 - 3)² = 1² = 1

The gradient of tangent is 4 at (2, 1 ) on the curve