Question

If f(x)=x^3-9,find lim f(x+h)-f(x)/h
h---->0

Answer 1

Hi! Your answer is 3x²

Please read an explanation for a clear understanding to the problem.

Any questions about the answer/explanation can be asked through comments! :)

Explanation:

Goal

• Find the limit of f(x+h)-f(x)/h when h --> 0

Given

• A Cubic Function

`\LARGE{f(x)=x^(3)-9}`

Step 1

• Rewrite the limit

`\LARGE{\lim_(h \to 0) (f(x+h)-f(x))/(h)}\\`

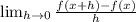
Since f(x) = x³-9. Therefore, f(x+h) would be (x+h)³-9

`\LARGE{\lim_(h \to 0) ([(x+h)^3-9]-(x^3-9))/(h)}`

Simplify the numerator

`\LARGE{\lim_(h \to 0) (x^3+3x^2h+3xh^2+h^3-9-x^3+9)/(h)}\\\LARGE{\lim_(h \to 0) (3x^2h+3xh^2+h^3)/(h)}`

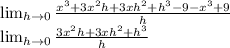
Step 2

• Factor the numerator so we don't let h = 0.

When finding a limit of function, we can't let the approaching variable equal to 0 (Unless if a function doesn't really have limits.)

`\LARGE{\lim_(h \to 0) (3x^2h+3xh^2+h^3)/(h)}\\\LARGE{\lim_(h \to 0) (h(3x^2+3xh+h^2))/(h)}`

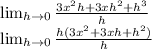
Cancel both h-term from denominator and numerator

`\LARGE{\lim_(h \to 0) (h(3x^2+3xh+h^2))/(h)}\\\LARGE{\lim_(h \to 0) (1(3x^2+3xh+h^2))/(1)}\\\LARGE{\lim_(h \to 0) (3x^2+3xh+h^2)`

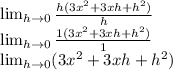
Step 3

• Substitute h = 0 in the expression.

`\LARGE{\lim_(h \to 0) (3x^2+3xh+h^2)}\\\LARGE{\lim_(h \to 0) (3x^2+3x(0)+0^2)}\\\LARGE{\lim_(h \to 0) (3x^2+0+0)}\\\LARGE{\lim_(h \to 0) 3x^2`

Since we can't proceed anymore, therefore. The answer is 3x²

Additional Information

• This is the limit method to find a derivative of function.
• To find a derivative for polynomial without using limit method, we can do by let exponent become a coefficient then subtract exponent by 1. For example, if you want to differentiate x³ the answer will be 3x².