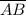Question

The verticies of the triangle OAB are the origin O, A(-15,0) and B(0,8)

What is the relationship between G and the triangle OAB

G(-7.5,4)
​

Answer 1

G is the midpoint of the side
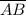`\overline {AB}` of triangle ΔOAB

Explanation:

The vertices of the triangle ΔOAB are A(-15, 0), B(0, 8), and C(0, 0)

The coordinates of the point G = (-7.5, 4)

The length from the point A to the point G,
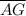`\overline {AG}` is given as follows;

`\overline {AG} =√((-7.5 - (-15))^2 + (4 - 0)^2) = √(7.5^2 + 4^2) = 8.5`

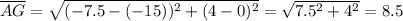
The length from the point A to the point B,
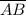`\overline {AB}` is given as follows;

`\overline {AB} =√((-15 - 0)^2 + (8 - 0)^2) = √(15^2 + 8^2) = 17`

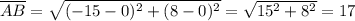
Therefore, the point G is the half way mark of
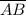`\overline {AB}` = The midpoint of the side
`\overline {AB}`