Answer:
E. None of the above.
Explanation:
The n-th root of a complex number can be calculated by the De Moivre's Theorem:
![z^(1/n) = r^(1/n)\cdot \left[\cos \left((\theta + 2\cdot k\cdot \pi)/(n) \right)+i\,\sin \left((\theta + 2\cdot k\cdot \pi)/(n)\right)\right]](https://img.qammunity.org/2022/formulas/mathematics/college/idfhpuvrvxa8m4wrka3dupcnpvku4gzs8v.png) , for
, for
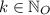 (1)
(1)
Where:
 - Grade of the root.
- Grade of the root.
 - Norm of the complex number.
- Norm of the complex number.
 - Direction of the complex number, measured in radians.
- Direction of the complex number, measured in radians.
 - Index of the solution.
- Index of the solution.
If we know that
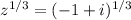 , then the root of the number is:
, then the root of the number is:
Norm
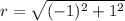
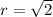
Direction
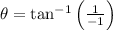
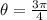
If
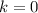 , then the root of this number is:
, then the root of this number is:
![z^(1/3) = 2^(1/6)\cdot \left[\cos \left(((3\pi)/(4) )/(3) \right)+i\,\sin \left(((3\pi)/(4) )/(3) \right)\right]](https://img.qammunity.org/2022/formulas/mathematics/college/a1txqq8yj2baswuu1n623rtyfimcvp4uml.png)
![z^(1/3) = 2^(1/6)\cdot \left[\cos (\pi)/(4)+i\,\sin (\pi)/(4) \right]](https://img.qammunity.org/2022/formulas/mathematics/college/wmjqmktpii5ml0q1fcfblyjj04a6k8it7y.png)
![z^(1/3) = 2^(1/6)\cdot \left[\cos 45^(\circ)+i\,\sin 45^(\circ)\right]](https://img.qammunity.org/2022/formulas/mathematics/college/80n0ljbkd7lktdkms7f6bqp8w1ccfomijj.png)
Hence, the right answer is E.