Answer:
The missing parts of the triangle are
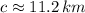 ,
,
 and
and
 , respectively.
, respectively.
Explanation:
A triangle is formed by three sides and three angles, a side and two angles are missing (
 ,
,
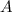 ,
,
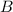 ).
).
The length of the missing side is found by the Law of Cosine:
 (1)
(1)
(
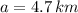 ,
,
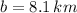 ,
,
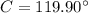 )
)
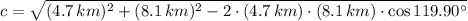
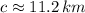
And the missing angles can be determined by the Law of Sine:
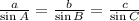
(
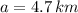 ,
,
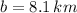 ,
,
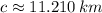 ,
,
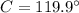 )
)
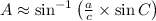
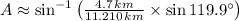

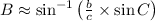
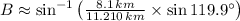

The missing parts of the triangle are
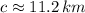 ,
,
 and
and
 , respectively.
, respectively.