Question

4. Find the missing parts of the triangle. Round to the nearest tenth when necessary or to the nearest minute as appropriate.

C = 119.90
a = 4.7 km
b = 8.1 km

Answer 1

The missing parts of the triangle are
`c \approx 11.2\,km`,
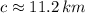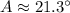`A\approx 21.3^(\circ)` and
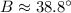`B \approx 38.8^(\circ)`, respectively.

Explanation:

A triangle is formed by three sides and three angles, a side and two angles are missing (
`c`,
`A`,
`B`).

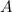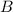The length of the missing side is found by the Law of Cosine:

`c = \sqrt{a^(2)+b^(2)-2\cdot a \cdot b\cdot \cos C}` (1)

(
`a = 4.7\,km`,
`b = 8.1\,km`,
`C = 119.90^(\circ)`)

`c = \sqrt{(4.7\,km)^(2)+(8.1\,km)^(2)-2\cdot (4.7\,km)\cdot (8.1\,km)\cdot \cos 119.90^(\circ)}`

`c \approx 11.2\,km`

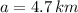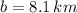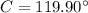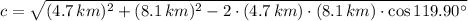
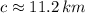
And the missing angles can be determined by the Law of Sine:

`(a)/(\sin A) = (b)/(\sin B) = (c)/(\sin C)`

(
`a = 4.7\,km`,
`b = 8.1\,km`,
`c \approx 11.210\,km`,
`C = 119.9^(\circ)`)

`A \approx \sin^(-1)\left((a)/(c) * \sin C \right)`

`A \approx \sin^(-1) \left((4.7\,km)/(11.210\,km)* \sin 119.9^(\circ) \right)`

`A\approx 21.3^(\circ)`

`B \approx \sin^(-1) \left((b)/(c)* \sin C \right)`

`B\approx \sin^(-1)\left((8.1\,km)/(11.210\,km)* \sin 119.9^(\circ) \right)`

`B \approx 38.8^(\circ)`

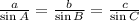
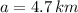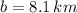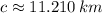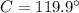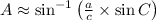
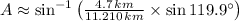
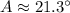
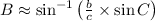
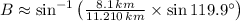
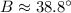
The missing parts of the triangle are
`c \approx 11.2\,km`,
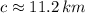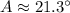`A\approx 21.3^(\circ)` and
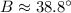`B \approx 38.8^(\circ)`, respectively.