Question

The smallest postive natural number n for which 125×n is a perfect square number​

Answer 1

Answer: 5

==========================================================

Step-by-step explanation:

125 = 5^3

If n = 5^p, where p is some positive whole number, then

125n = 5^3*5^p = 5^(3+p)

So that's why I made n some power of 5.

To be a perfect square, the exponent 3+p must be even

Since we want 125n to be as small as possible, we'll go with the smallest possible p here which is p = 1. Note how 3+p = 3+1 = 4 is even.

Furthermore, note that 5^(3+p) = 5^4 = 625

The square root of 625 is 25

We could write it like this

`√(5^4) = √((5^2)^2) = 5^2 = 25`

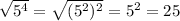
Showing that 5^4 = 625 is a perfect square number.

So because p = 1, this makes n = 5^p = 5^1 = 5.

Answer 2

125+19= 144=12^2 is the answer.

Step-by-step explanation:

Hope it will be helpful.