Question

Each statement describes a transformation of the graph of y= x. Which statement correctly describes the graph of y= x - 8?

Answer 1

The function
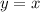`y = x` is shifted downwards by 8 units

Explanation:

Given

`y = x`

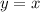
Required

Determine the transformation that gives:
`y = x-8`

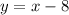
When a function f(x) is shifted by b units, the new function g(x) is g(x) = f(x) - b

In this case:

`y = x`

`b = 8`

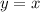
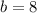
So, the new function is:

`y = x - b`

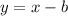
Substitute 8 for b

`y = x - 8`

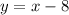
Hence, the function is shifted 8 units downward