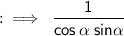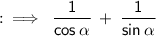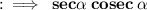Question

Prove the following identities : i) tan a + cot a = cosec a sec a​

Answer 1

Explanation:

`\tan \alpha + \cot\alpha = (\sin \alpha)/(\cos \alpha) +(\cos \alpha)/(\sin \alpha)`

`=(\sin^2\alpha + \cos^2\alpha)/(\sin\alpha\cos\alpha)=(1)/(\sin\alpha\cos\alpha)`

`=\left((1)/(\sin\alpha)\right)\!\left((1)/(\cos\alpha)\right)=\csc \alpha \sec\alpha`

Answer 2

Question :

• tan alpha + cot Alpha = cosec alpha. sec alpha

Required solution :

Here we would be considering L.H.S. and solving.

Identities as we know that,

• 
  `\red{\boxed{\sf{tan \: \alpha \: = \: (sin \: \alpha )/(cos \: \alpha) }}}`
• 
  `\red{\boxed{\sf{cot \: \alpha \: = \: (cos \: \alpha )/(sin \: \alpha) }}}`

By using the identities we gets,

`: \: \implies \: \sf{ (sin \: \alpha )/(cos \: \alpha) \: + \: (cos \: \alpha )/(sin \: \alpha) }`

`: \: \implies \: \sf{ (sin \: \alpha * sin \: \alpha )/(cos \: \alpha * sin \: \alpha) \: + \: (cos \: \alpha * cos \: \alpha )/(sin \: \alpha * \: cos \: \alpha ) }`

`: \: \implies \: \sf{ \frac{sin {}^(2) \: \alpha }{cos \: \alpha * sin \alpha} \: + \: \frac{cos {}^(2) \: \alpha }{sin \: \alpha * \: cos \: \alpha } }`

`: \: \implies \: \sf{ \frac{sin {}^(2) \: \alpha }{cos \: \alpha \: sin \alpha} \: + \: \frac{cos {}^(2) \: \alpha }{sin \: \alpha \: cos \: \alpha } }`

`: \: \implies \: \sf{ \frac{sin {}^(2) \: \alpha \: + \: cos {}^(2) \alpha}{cos \: \alpha \: sin \alpha} }`

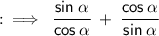
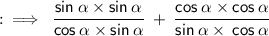
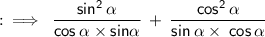
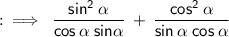
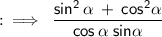
Now, here we would be using the identity of square relations.

• 
  `\red{\boxed{ \sf{sin {}^(2) \alpha \: + \: cos {}^(2) \alpha \: = \: 1}}}`

By using the identity we gets,

`: \: \implies \: \sf{ (1)/(cos \: \alpha \: sin \alpha) }`

`: \: \implies \: \sf{ (1)/(cos \: \alpha ) \: + \: (1)/(sin\: \alpha) }`

`: \: \implies \: \bf{sec \alpha \: cosec \: \alpha}`

• Hence proved..!!