Question

Two of the vertices of a triangle (0,1) and (4,1). Which coordinates of the third vertex make the area of the triangle equal 16

Answer 1

If triangle is a right triangle, then four possible solutions exist: 1) (0, 10), 2) (0, - 8), 3) (4, 10), 4) (4, - 8)

Explanation:

Let suppose that figure is a right triangle. Geometrically speaking, the area of the triangle is represented by the following formula:

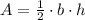`A = (1)/(2)\cdot b\cdot h` (1)

Where:

`b` - Base.

`h` - Height.

`A` - Area of the triangle.

Besides, let consider that line segment is between (0, 1) and (4, 1). The length of the base is determined by Pythagorean Theorem:

`b = \sqrt{(4-0)^(2)+(1-1)^(2)}`

`b = 4`

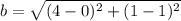
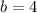
If we know that
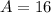`A = 16` and
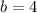`b = 4`, then the height of the triangle is:

`h = (2\cdot A)/(b)`

`h = 9`

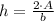
There are four possible solutions for the coordinates of the vertex of the triangle:

1) (0, 10), 2) (0, - 8), 3) (4, 10), 4) (4, - 8)