Given:
In a set of 3 numbers the first is a positive integer, the second is 3 more than the first and the 3rd is a square of the second.
To find:
The equation for the given situation if the sum of the numbers is 77.
Solution:
a. Let the first number in the set is x.
The second is 3 more than the first. So, the second number is
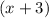 .
.
The 3rd number is a square of the second. So, the third number is
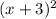 .
.
Therefore, the first, second and third numbers are
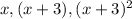 respectively.
respectively.
b. The sum of the numbers is 77.
First number + Second number + Third number = 77
c. So, the equation in terms of x is:
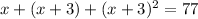
Therefore, the required equation is
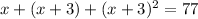 .
.
d. On simplification, we get
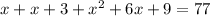
![[\because (a+b)^2=a^2+2ab+b^2]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/fpskn1z17avxoz8no22crt.png)
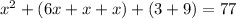
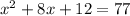
Subtract 77 from both sides.
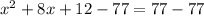
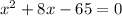
Therefore, the simplified form of the required equation is
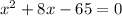 .
.