Question

Please help me with this problem!!

Answer 1

m∠3 = 33°

Explanation:

Given that ∠1, ∠2, and ∠3 are adjacent angles, and that ∠1 and ∠2 are supplementary, while ∠2 and ∠3 are complementary angles.

We are also given the values for the following angles:

m∠1 = (8x + 3)°

m∠2 = (5x - 18)°

In order to find the measure of ∠3, we must first find the value of x using the details from the given prompt.

We know that ∠1 and ∠2 are supplements, which means that the sum of their measures add up to 180°. In other words:

m∠1 + m∠2 = 180°

Substitute the given values into the equation:

(8x + 3)° + (5x - 18)° = 180°

8x° + 3° + 5x° - 18° = 180°

Combine like terms:

13x° - 15° = 180°

Add 15° from both sides:

13x° - 15° + 15° = 180° + 15°

13x° = 195°

Divide both sides by 13 to solve for x:

`\displaystyle\mathsf{(13x^(\circ))/(13^(\circ))\:=\:(195^(\circ))/(13^(\circ)) }`

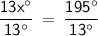
x = 15°

Now that we have the value for x = 15°, we need to determine the measure of ∠3. Using the details from the given prompt that m∠2 and m∠3 are complementary angles (whose measures add up to 90°), then we can set up the following equation:

m∠2 + m∠3 = 90°

Substitute its value into m∠2° to find the m∠3°.

m∠2 + m∠3 = 90°

(5x - 18)° + m∠3 = 90°

5(15)° - 18° + m∠3 = 90°

75° - 18° + m∠3 = 90°

57° + m∠3 = 90°

Subtract 57° from both sides:

57° - 57° + m∠3 = 90° - 57°

m∠3 = 33°

Therefore, the measure of ∠3 is 33°.

Double-check:

In order to verify whether we have the correct measure for ∠3, we'll substitute the x = 15° into the given values for ∠1, ∠2, and the derived value for ∠3.

m∠1 + m∠2 = 180°

(8x + 3)° + (5x - 18)° = 180°

8(15)° + 3° + 5(15)° - 18° = 180°

120° + 3° + 75° - 18° = 180°

180° = 180° (True statement).

m∠2 + m∠3 = 90°

(5x - 18)° + 33° = 90°

5(15)° - 18° + 33° = 90°

75° - 18° + 33° = 90°

90° = 90° (True statement).