Question

ABCD is a rectangle formed by the points A( -1, -1 ), B( -1, 4), C(5,4), D(5, -1).P,Q,R and S are the mid points of AB,BC,CD and DA respectively.Prove that PQRS is a rhombus.

Answer 1

Proved

Explanation:

Given

`A = (-1,-1)`

`B = (-1,4)`

`C = (5,4)`

`D = (5,-1)`

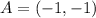
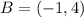
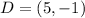
Required

Prove that PQRS is a rhombus

P = midpoint of AB

So:

`P = (1)/(2)(-1-1,-1+4)`

`P = (1)/(2)(-2,3)`

`P = (-1,(3)/(2))`

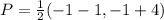
Q = midpoint of BC

`Q = (1)/(2)(-1+5,4+4)`

`Q = (1)/(2)(4,8)`

`Q = (2,4)`

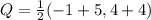
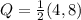
R = midpoint of CD

`R =(1)/(2)(5+5,4-1)`

`R =(1)/(2)(10,3)`

`R = (5,(3)/(2))`

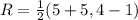
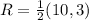
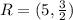
S = midpoint of DA

`S = (1)/(2)(5-1,-1-1)`

`S = (1)/(2)(4,-2)`

`S = (2,-1)`

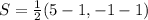
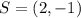
So, we have:

`P = (-1,(3)/(2))`

`Q = (2,4)`

`R = (5,(3)/(2))`

`S = (2,-1)`

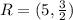
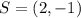
To show that PQRS is a rhombus, the distance between PQ, QR, RS and SW must be equal.

Distance is calculated as:

`D = √((x_1-x_2)^2 + (y_1-y_2)^2)`

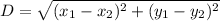
For PQ

`D_1 = \sqrt{(-1-2)^2 + ((3)/(2)-4)^2}`

`D_1 = \sqrt{(-3)^2 + (-(5)/(2))^2}`

`D_1 = \sqrt{9 + (25)/(4)}`

`D_1 = \sqrt{(61)/(4)}`

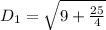
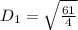
For QR

`D_2 = \sqrt{(2-5)^2 + (4-(3)/(2))^2}`

`D_2 = \sqrt{(-3)^2 + ((5)/(2))^2}`

`D_2 = \sqrt{9 + (25)/(4)}`

`D_2 = \sqrt{(61)/(4)}`

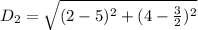
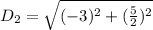
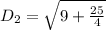
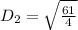
For RS

`D_3 = \sqrt{(5-2)^2 + ((3)/(2)-(-1))^2}`

`D_3 = \sqrt{(5-2)^2 + ((3)/(2)+1)^2}`

`D_3 = \sqrt{(3)^2 + ((5)/(2))^2}`

`D_3 = \sqrt{9 + (25)/(4)}`

`D_3 = \sqrt{(61)/(4)}`

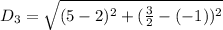
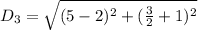
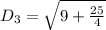
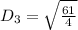
For SP

`D_4 = \sqrt{(2-(-1))^2+((3)/(2)-(-1))^2}`

`D_4 = \sqrt{(2+1))^2+((3)/(2)+1)^2}`

`D_4 = \sqrt{(3)^2 + ((5)/(2))^2}`

`D_4 = \sqrt{9 + (25)/(4)}`

`D_4 = \sqrt{(61)/(4)}`

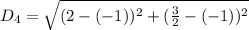
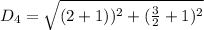
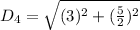
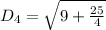
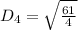
From the calculations above:

`D_1 =D_2 =D_3 =D_4 = \sqrt{(61)/(4)}`

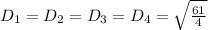
Hence: PQRS is a rhombus