Answer:
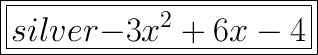
Explanation:
to understand this
you need to know about:
- algebra
- algebraic addition subtraction
- PEMDAS
tips and formulas:
- quadratic expression standard form:ax²+bx+c
- order of PEMDAS
- parentheses
- exponent
- multiplication or
- division
- addition
- subtraction
given:
to do
let's do:
![step - 1 : define]()
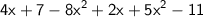
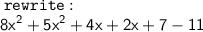
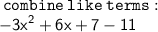
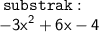
therefore
we can see the expression is in standard form since a,b and c is -3,6 and -4
also let's justify it
substitute the value of a,b and c respectively
(-3)x²+(6)x+(-4)
-3x²+6x-4 (proven)