Answer:

General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Equality Properties
- Multiplication Property of Equality
- Division Property of Equality
- Addition Property of Equality
- Subtraction Property of Equality
Explanation:
Step 1: Define
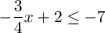
Step 2: Solve for x
- [Subtraction Property of Equality] Isolate x term:
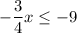
- [Division Property of Equality] Isolate x:

Here we see that any value x smaller than or equal to 12 would work as a solution to the inequality.