Answer:
A.]A chord of a circle of diameter 40 cm subtends an angle of 70° at the centre of the circle.
Solution given;
diameter [d]=40cm
centre angle [C]=70°
(a) Find the perpendicular distance be tween the chord and the centre of the circle.
Answer:
we have
the perpendicular distance be tween the chord and the centre of the circle=[P]let
we have
P=d Sin (C/2)
=40*sin (70/2)
=22.9cm
the perpendicular distance be tween the chord and the centre of the circle is 22.9cm.
(b) Using = 3.142, find the length of the minor arc.
Solution given;
minor arc=
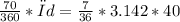
=24.44cm
the length of the minor arc. is 24.44cm.
B.]In the diagram, XZ is a diameter of the cir cle XYZW, with centre O and radius 15/2 cm.
If XY = 12 cm, find the area of triangle XYZ.
Solution given:
XY=12cm
XO=15/2cm
XZ=2*15/2=15cm
Now
In right angled triangle XOY [inscribed angle on a diameter is 90°]
By using Pythagoras law
h²=p²+b²
XZ²=XY²+YZ²
15²=12²+YZ²
YZ²=15²-12²
YZ=
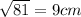
:.
base=9cm
perpendicular=12cm
Now
Area of triangle XYZ=½*perpendicular*base
=½*12*9=54cm²
the area of triangle XYZ is 54cm².