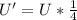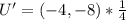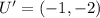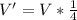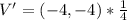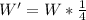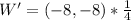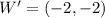Answer:
See Explanation
Explanation:
Given
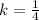 --- scale factor
--- scale factor
Required
Determine possible new vertices
The vertices of
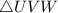 is not given. So, I will answer the question based on an assumed vertex for
is not given. So, I will answer the question based on an assumed vertex for
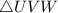
Given that the scale factor is 1/4, the relationship between
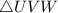 and
and
 is:
is:
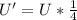
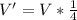
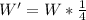
Assumptions:
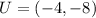
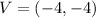

So, the possible vertices are: