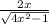Question

Find the exact value of the composite function show work​

Answer 1

`\frac{2x}{\sqrt{4x^(2) -1} }`

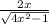
Explanation:

This function can be written as:

`(1)/(cos(sin^(-1)((1)/(2x))) )`

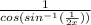
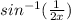`sin^(-1)((1)/(2x))` means the angle whose sine is 1/(2x). This implies that the denominator is the cosine of the angle whose sine is 1/(2x)

Think of a right triangle and consider the angle with this sine. Then the opposite side has length 1 and the hypotenuse has length 2x. The Pythagorean theorem then implies that the adjacent side is

`\sqrt{4x^(2) -1}`

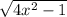
The cosine of the angle is adjacent over hypotenuse, so the cosine is

`\frac{\sqrt{4x^(2) -1}}{2x}`

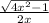
The secant is the inverse of the cosine, so the answer is

`\frac{2x}{\sqrt{4x^(2) -1} }`