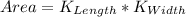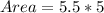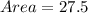Question

Rectangles J and K are similar. If the area of rectangle J is 440, what is the area of rectangle K? I need this today

Answer 1

`Area = 27.5`

Explanation:

Given

`J_(Area) = 440`

`J_(Width) = 22`

`K_(Width) = 5.5`

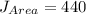
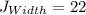
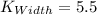
See attachment

Required

Determine the area of K

First, we need to calculate the length of the rectangle J

`J_(Length) * J_(Width) = J_(Area)`

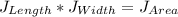
This gives:

`J_(Length) * 22 = 440`

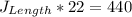
Divide both sides by 22

`(J_(Length) * 22)/(22) = (440)/(22)`

`J_(Length) = 20`

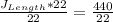
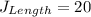
So, the length of the rectangle J is 20.

Since both shapes are similar, then:

`J_(Length) : J_(Width) = K_(Length) : `K_(Width)`

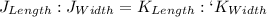
Substitute the known values:

`20 : 22 = K_(Length) : `5.5`

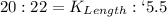
Express as fraction:

`(20 )/( 22 )= (K_(Length) )/( `5.5)`

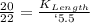
Make Length, the subject of formula

`K_(Length) = (5.5 * 20)/(22)`

`K_(Length) = (110)/(22)`

`K_(Length) = 5`

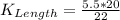
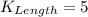
The area of K is:

`Area = K_(Length) * K_{Width`

`Area = 5.5 * 5`

`Area = 27.5`