Question

(7).Given f(x) =


`(1)/(x ^(2) - 1)`
and g(x)=

`(x)/(x + 2)`
where x & R.

Find the ;
(i). inverse of g(x) (ii). Expression

`g{x} ^( - 1) f{x}`

iii). Largest domain of f(x) and g(x) respectively.​

Answer 1

The inverse of g(x) is
`g^(-1)(x)=(2x)/(1-x)`

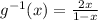
The domain of g(x) is (-∞,-2)U(-2,∞)

The domain of f(x) is (-∞,-1)U(-1,1)U(1,∞)

Explanation:

Find the inverse of g(x).

`y=(x)/(x+2)`

Solve for x

`x=y(x+2)`

`x=xy+2y`

`x(1-y)=2y`

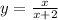
`x=(2y)/(1-y)`

`g^(-1)(x)=(2x)/(1-x)`

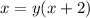
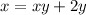
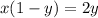
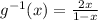
Find the domain of g(x)

`g(x)=(x)/(x+2)`

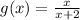
Numerator and denominator have domain

(-∞,∞).

However, g(x) is undefined if the denominator is 0. Hence, x=-2 must be taken out of the domain. So, the domain of g(x) is

(-∞,-2)U(-2,∞).

Find the domain of f(x)

`f(x)=(1)/(x^(2) -1)`

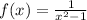
The numerator and denominator have the domain

(-∞,∞)

However, f(x) is undefined if the denominator is 0. This rules out +1 and -1. So, the domain of f(x) is

(-∞,-1)U(-1,1)U(1,∞)

I am not sure what you mean for (ii).