Answer: v = 0.6 m/s
Step-by-step explanation: Momentum Conservation Principle states that for a collision between two objects in an isolated system, the total momentum of the objects before the collision is equal to the total momentum of the objects after the collision.
Momentum is calculated as Q = m.v
For the piñata problem:
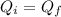
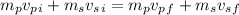
Before the collision, the piñata is not moving, so
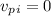 .
.
After the collision, the stick stops, so
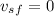 .
.
Rearraging, we have:
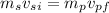
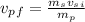
Substituting:
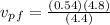
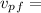 0.6
0.6
Immediately after being cracked by the stick, the piñata has a swing speed of 0.6 m/s.