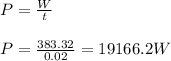Question

A cylinder of volume 3 liter has Argon gas initially at 300 K, and 1.00 atm pressure. The piston compresses the gas to a new pressure of 3.60 atm. During this compression, the temperature is maintained constant by using an appropriate heat sink. Find (a) the final volume of the gas, (b) the work done on the gas by the piston, (c) the energy transferred out by heat.(d) If the process takes 20 milliseconds, what is the power

Answer 1

(a) 0.833 L

(b) - 383.32J

(c) - 383.32 J

(d) 19166.2 W

Step-by-step explanation:

initial volume, V = 3 L

initial temperature, T = 300 K

Initial pressure, P = 1 atm

final pressure, P' = 3.6 atm

Temperature is constant.

(a) Let the final volume is V'.

As the temperature is constant,

P V = P' V'

1 x 3 = 3.6 x V'

V' = 0.833 L

(b) Let the number of moles is n

`P V = n R T \\\\1* 1.01 * 10^5* 3* 10^(-3) = n* 8.31* 300\\\\n = 0.12`

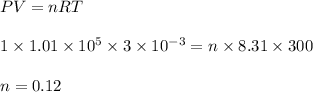
The work done in isothermal process is

`W = n T T lon{(V')/(V)}\\\\W = 0.12 * 8.31* 300* ln {(0.833)/(3)}\\\\W = - 383.32 J`

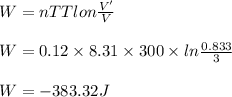
(c) The energy is given by the first law of thermodynamics

dQ = dU + dW

Here, dU is the zero as the temperature is constant.

So, the heat energy is

dQ = dW = - 383.32 J

(d) Time, t = 20 ms

Power is

`P = (W)/(t) \\\\P = (383.32)/(0.02) =19166.2 W`

Answer 2

Step-by-step explanation:

Apply Boyle's law of gas

P₁ V₁ = P₂ V₂ where P₁ and P₂ are initial and final pressure , V₁ , V₂ are initial and final volume .

1.00 atm x 3 liter = 3.60 atm x V₂

V₂ = 0.833 liter.

b )

Work done on the gas by piston = 2.303 RT log P₂ / P₁

= 2.303 x 8.3 x 300 K x log 3.6 atm / 1 atm

= 3190 J .

c )

Q = ΔE + W

Q = 0 + 3190 J

Heat energy transferred out Q = 3190 J

d )

Power = work done / time

= 3190 J / .020 second

= 159500 W .

159.5 kW.