Question

Quit smoking: In a survey of 444 HIV-positive smokers, 202 reported that they had used a nicotine patch to try to quit smoking. Can you conclude that less than half of HIV-positive smokers have used a nicotine patch

Answer 1

The p-value of the test is of 0.0287 < 0.05(standard significance level), which means that it can be concluded that less than half of HIV-positive smokers have used a nicotine patch.

Explanation:

Test if less than half of HIV-positive smokers have used a nicotine patch:

At the null hypothesis, we test if the proportion is of at least half, that is:

`H_0: p \geq 0.5`

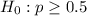
At the alternative hypothesis, we test if the proportion is below 0.5, that is:

`H_1: p < 0.5`

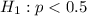
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

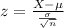
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
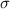`\sigma` is the standard deviation and n is the size of the sample.

0.5 is tested at the null hypothesis:

This means that
`\mu = 0.5, \sigma = √(0.5*(1-0.5)) = 0.5`

In a survey of 444 HIV-positive smokers, 202 reported that they had used a nicotine patch to try to quit smoking.

This means that
`n = 444, X = (202)/(444) = 0.455`

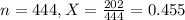
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.455 - 0.5)/((0.5)/(√(444)))`

`z = -1.9`

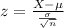
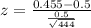
P-value of the test and decision:

The p-value of the test is the probability of finding a sample proportion below 0.455, which is the p-value of z = -1.9.

Looking at the z-table, z = -1.9 has a p-value of 0.0287.

The p-value is of 0.0287 < 0.05(standard significance level), which means that it can be concluded that less than half of HIV-positive smokers have used a nicotine patch.