Question

PLEASE HELP THIS IS TIMED

A salesperson receives a 3% commission on sales. The salesperson receives $180 in commission. What is the amount of sales?

Thank you :)

Answer 1

$6,000

Explanation:

Form an equation

let s be the amount of sales

You know that the salesperson gets 3%, or 0.03 of the sales, so:

0.03x = 180

Then, solve

`0.03x=180`

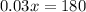
multiply both sides by 100 to get rid of the decimal

`3x=18000`

divide both sides by 3

`x=6000`

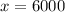
So the amount of sales is $6,000