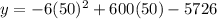Question

PLEASE HELP!!! (question is in image)

Answer 1

Explanation:

We can find the maximum profit by taking the derivative of the profit and then solving for the widget price x that will maximize it. It is done by equating the derivative to zero:

`(dy)/(dx) = -12x + 600 = 0`

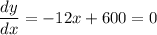
Solving for x, we get

`x = (600)/(12) = \$50`

By setting the widget price to $50, the company can maximize their profits. To find this maximum profit, substitute the value of x into the equation for the profit:

`y = -6(50)^2 + 600(50) - 5726`

`\;\;\;=\$9,274`