Question

The probability that Barry Bonds hits a home run on any given at-bat is 0.16, and each at-bat is independent.

Part A: What is the probability that the next home run will be on his fifth at-bat? (5 points)

Part B: What is the expected number of at-bats until the next home run? (5 points)

Answer 1

a) 0.0797 = 7.97% probability that the next home run will be on his fifth at-bat.

b) The expected number of at-bats until the next home run is 6.25.

Explanation:

For each at bat, there are two possible outcomes. Either it is a home run, or it is not. The probability of an at bat resulting in a home run is independent of any other at-bat, which means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

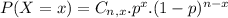
In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

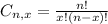
And p is the probability of X happening.

The probability that Barry Bonds hits a home run on any given at-bat is 0.16

This means that
`p = 0.16`

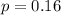
Part A: What is the probability that the next home run will be on his fifth at-bat?

0 on his next 4(P(X = 0) when n = 4)

Home run on his 5th at-bat, with 0.16 probability. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(4,0).(0.16)^(0).(0.84)^(4) = 0.49787136`

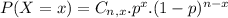
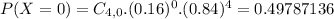
0.49787136 *0.16 = 0.0797.

0.0797 = 7.97% probability that the next home run will be on his fifth at-bat.

Part B: What is the expected number of at-bats until the next home run?

The expected number of trials for n successes is given by:

`E = (n)/(p)`

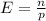
In this question,
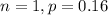`n = 1, p = 0.16`. So

`E = (1)/(0.16) = 6.25`

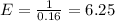
The expected number of at-bats until the next home run is 6.25.