Question

Use special right triangle ratios to find the lengths of the other leg and the hypotenuse

Answer 1

the lengths of the other leg and the hypotenuse

is 18 units and 18
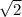`√(2)`units respectively.

Answer:

Solution given:

Let <C=<B=45°

AB=18 units

BC=?

AC=?

again

By using

By usingspecial right triangle ratios

sin C=opposite/hypotenuse=AB/AC=18/AC

Sin 45=18/AC

AC=18/sin45

AC=hypotenuse=18
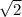`√(2)`units

again

Tan A=opposite/adjacent=BC/AB=BC/18

Tan45=BC/18

BC=Tan45*18

BC=length of another leg=18 units.

Answer 2

leg = 18

hypotenuse = 18 sqrt(2)

Explanation:

We know that sin theta = opp side / hypotenuse

sin 45 = 18 / hyp

hyp sin 45 = 18

hyp = 18 / sin 45

hyp = 18 sqrt(2)

Since this is an isosceles triangle ( the two angles are the same measure), the two legs have to be the same length

leg = 18