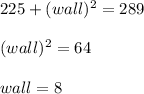Question

A 17 feet ladder is placed against a building. The bottom of the ladder is 15 feet away from the building. How many feet high is the top of the ladder?

7 feet
12 feet
8 feet
15 feet

Answer 1

`8 \ feet`

Explanation:

In this situation, one is given the following information. A ladder is leaning against a wall and has a measure of (17) feet. The bottom of the ladder is (15) feet away from the wall. One can infer that the wall forms a right angle with the ground. Thus, the triangle formed between the ground, ladder, and wall is a right triangle. Therefore, one can use the Pythagorean theorem. The Pythagorean theorem states the following,

`a^2+b^2=c^2`

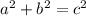
Where (a) and (b) are the legs or the sides adjacent to the right angle of the right triangle. The parameter (c) represents the hypotenuse or the side opposite the right angle. In this case, the legs are the ground and wall, and the hypotenuse is the ladder. Substitute this into the formula a solve for the height of the wall.

`a^2+b^2=c^2`

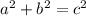
Substitute,

`(ground)^2+(wall)^2=(ladder)^2\\\\(15)^2+(wall)^2=(17)^2\\`

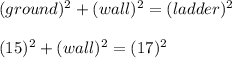
Simplify,

`(15)^2+(wall)^2=(17)^2\\\\225+(wall)^2=289`

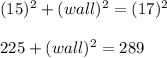
Inverse operations,

`225+(wall)^2=289\\\\(wall)^2=64\\\\wall=8`