Answer:
The remaining area of the original rectangle can be expressed as: length = 11x + 5 & width = 5x - 7
Explanation:
Jason cut a square out of a rectangle which means the new rectangle will be smaller than the original one. To find the new length and width of the rectangle, we subtract (x + 2) from the original length and width respectively. So we'll have:
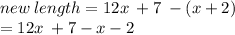
When you expand and open the bracket, (x + 2) will become - x - 2. Now, collect like terms:

The new length will be = 11x + 5
To find the new width of the rectangle, we'll have:
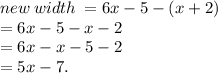
So we have (5x - 7) as the new width.