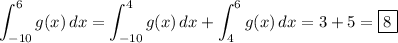We're given

which immediately tells us that
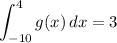
In other words, swapping the limits of the integral negates its value.
Also,
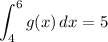
The integral we want to compute is
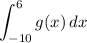
which we can do by splitting up the integral at x = 4 and using the known values above. Then the integral we want is