Question

A particular airport has beacons on the ground 5 km out from the start of each runway. An airplane is directly over this beacon and is at an angle of elevation from the runway of 9°. Calculate the direct line distance from the airplane to the start of the runway

Answer 1

The direct distance from the plane to the start of the runway is approximately 5.0623 km

Explanation:

The locations of the beacons on the runway, x = 5 km from the start of each runway

The angle of elevation of the airplane from the runway, θ = 9°

Let 'R' represent the direct distance from the plane to the start of the runway

The horizontal distance from the start of the runway to the beacon, 'x', the distance from the plane to the start of the runway, 'R', and the vertical height of the plane, 'h' form a right triangle with rides x, R, and h

By trigonometric ratios, we have;

`cos\angle \theta = (The \ length \ of \ the \ adjacent\ leg \ to \ \angle \theta)/(The \ length \ of \ the \ hypotenuse \ side) = (x)/(R)`

Therefore, we have;

`cos (9 ^(\circ)) = (x)/(R) = (5)/(R)`

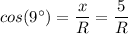
From which we have;

`R= (5)/(cos (9 ^(\circ)) ) \approx 5.0623`

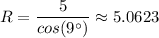
The direct distance from the plane to the start of the runway, R ≈ 5.0623 km