Question

Anas wants to build a one-sample z interval with 85% confidence to estimate what proportion of users will click an advertisement that appears on his website. He takes a random sample of 250 users and finds that 54 of them clicked the advertisement. Answer the following:

1. What critical value z start superscript, times, end superscript should Anas use to construct this confidence interval?

2. Provide the value of margin of error.

3. Provide the confidence interval with 85% of confidence.

4. What would happen if Anas managed to have 500 sample size?

Answer 1

See below

Explanation:

Check One Sample Z-Interval Conditions

Simple Random Sample? √

np≥10? √

n(1-p)≥10? √

One-Sample Z-Interval Information

• Formula -->
  `CI=\hat{p}\pm z^*\biggr(\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\biggr)`
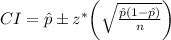
• Sample Proportion -->
  `\hat{p}=(54)/(250)=0.216`
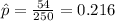
• Critical Value -->
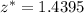  `z^*=1.4395` (for a 85% confidence level)
• Sample Size -->
  `n=250`
• Margin of Error (MOE) -->
  `\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

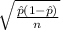
Problem 1

As stated previously, Anas should use the critical value
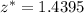`z^*=1.4395` to construct the 85% confidence interval

Problem 2

Given our formula for the margin of error (MOE), the value is
`MOE=\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}=\sqrt{(0.216(1-0.216))/(250)}\approx0.026`

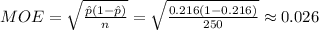
Problem 3

The 85% confidence interval would be
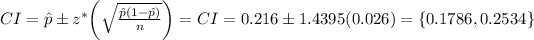`CI=\hat{p}\pm z^*\biggr(\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\biggr)=CI=0.216\pm 1.4395(0.026)\appro=\{0.1786,0.2534\}`, which means that we are 85% confident that the true proportion of people that clicked on the advertisement is between 0.1786 (~45 people) and 0.2534 (~63 people)

Problem 4

Increasing the sample size to
`n=500` is going to decrease the margin of error because it is a closer representation of the population, but, alas, requires more time, energy, and resources to observe.