Answer:
Explanation:
The easiest way to solve this is with calculus, believe it or not. The position function is
 . The first derivative of this is the velocity function:
. The first derivative of this is the velocity function:
v(t) = -32t + 64. From physics, we know that at the max height of an object's path, the velocity is equal to 0, so setting this velocity equation equal to 0 and solving for time, will tell us the time it took to get to the max height (which we don't know yet, but we will in a bit):
0 = -32t + 64 and
-64 = -32t so
t = 2 seconds. It takes 2 seconds to reach a max height. Plugging that 2 in for t in the position function will tell you the max height that corresponds to this time:
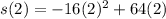 and
and
s(2) = 64 feet.
So the max height is 64 feet and it is reached at 2 seconds after launching.
Also from physics we know that at halfway through a parabolic path, which is also the max height, we are halfway through time-wise as well. That means that if it takes 2 seconds to reach the max height from the ground, it will take another 2 seconds to fall to the ground.
So the total time the rocket is in the air is 4 seconds: 2 seconds to reach the max height and another 2 to fall back down.