Question

12.36Un balón lleno contiene 12 kg de oxígeno, O2, bajo una presión ma-nométrica de 40 atm. Determine la masa de oxígeno que se ha extraído del balón cuando la presión absoluta alcanza el valor de 25 atm. Su-ponga que la temperatura del balón permanece constante. R: 7.3 kg.

Answer 1

Quedan 7.317 kilogramos de oxígeno en el balón y se extraen 4.683 kilogramos de oxígeno en el proceso.

Step-by-step explanation:

Asúmase que el balón es rígido. Supongamos que el oxígeno se comporta como un gas ideal, entonces la ecuación de estado es la siguiente:

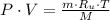`P\cdot V = (m\cdot R_(u)\cdot T)/(M)` (1)

Donde:

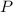`P` - Presión, medida en atmósferas.

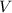`V` - Volumen, medido en litros.

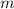`m` - Masa, medida en kilogramos.

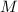`M` - Masa molar, medida en kilogramos por kilomol.

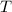`T` - Temperatura, medida en Kelvin.

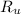`R_(u)` - Constante de los gases ideales, medida en atmósfera-litros por kilomol-Kelvin.

El aire experimenta un proceso isocórico e isotérmico, entonces obtenemos la siguiente relación:

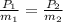`(P_(1))/(m_(1)) = (P_(2))/(m_(2))` (2)

Nótese que los subíndices 1 y 2 representan los estados inicial y final de proceso.

Si sabemos que
`P_(1) = 41\,atm`,
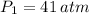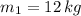`m_(1) = 12\,kg` y
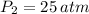`P_(2) = 25\,atm`, entonces la masa final del aire es:

`m_(2) = (P_(2))/(P_(1)) \cdot m_(1)`

`m_(2) = \left((25\,atm)/(41\,atm)\right)\cdot (12\,kg)`

`m_(2) = 7.317\,kg`

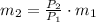
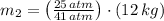
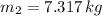
La masa que se ha extraído del balón es:

`\Delta m = m_(1)-m_(2)`

`\Delta m = 12\,kg-7.317\,kg`

`\Delta m = 4.683\,kg`

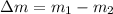
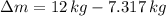
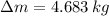
Quedan 7.317 kilogramos de oxígeno en el balón y se extraen 4.683 kilogramos de oxígeno en el proceso.