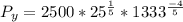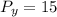Answer:
(a) 20226 units
(b) Marginal productivities
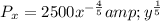
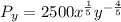
(c) Evaluation of the marginal productivities

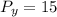
Explanation:
Given
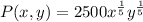
Solving (a): P(x,y) when x = 26 and y = 1333
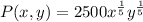 becomes
becomes
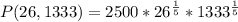
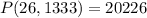 --- approximated
--- approximated
Solving (b): The marginal productivities
To do this, we simply calculate Px and Py
Differentiate x to give Px, so we have:
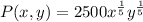 becomes
becomes
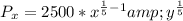
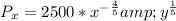
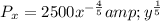
Differentiate y to give Py, so we have:
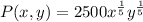 becomes
becomes
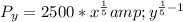
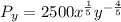
Solving (c): Px and Py when x = 25 and y = 1333
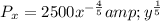 becomes
becomes
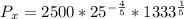
 --- approximated
--- approximated
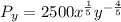 becomes
becomes