The function
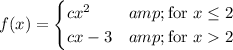
is piecewise continuous, since both cx ² and cx - 3 are polynomials. f(x) itself is continuous if both pieces meet at the same defined point. In other words, the limits of f(x) as x → 2 from either side have the same value of f (2) = c•2² = 4c.
We have
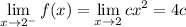

so in order for f to be continuous, we need
4c = 2c - 3 → 2c = -3 → c = -3/2