Answer:
Procedure:
1) Form a system of 3 linear equations based on the two zeroes and a point.
2) Solve the resulting system by analytical methods.
3) Substitute all coefficients.
Explanation:
A quadratic function is a polynomial of the form:
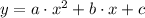 (1)
(1)
Where:
 - Independent variable.
- Independent variable.
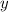 - Dependent variable.
- Dependent variable.
 ,
,
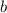 ,
,
 - Coefficients.
- Coefficients.
A value of
 is a zero of the quadratic function if and only if
is a zero of the quadratic function if and only if
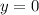 . By Fundamental Theorem of Algebra, quadratic functions with real coefficients may have two real solutions. We know the following three points:
. By Fundamental Theorem of Algebra, quadratic functions with real coefficients may have two real solutions. We know the following three points:
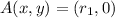 ,
,
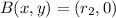 and
and
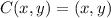
Based on such information, we form the following system of linear equations:
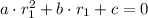 (2)
(2)
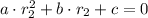 (3)
(3)
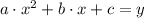 (4)
(4)
There are several forms of solving the system of equations. We decide to solve for all coefficients by determinants:
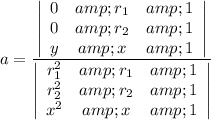
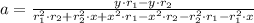
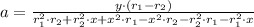
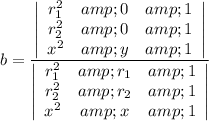
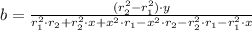
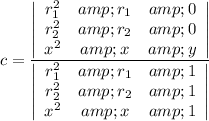
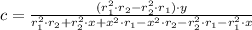
And finally we obtain the equation of the quadratic function given two zeroes and a point.