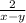Question

Do the indicated operations, express your answers in lowest terms

Answer 1

`(2)/(x-y)}`

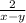
Explanation:

This equation may look difficult, but let's take it step by step. We are given the equation
`(3x+3y)/(x^(2)-y^(2) ) -(1)/(x-y)`.

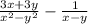We can simplify this to
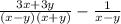`(3x+3y)/((x-y)(x+y)) -(1)/(x-y)` through the difference of two squares formula. Now, we need to make the denominators the same, so:

`(3x+3y)/((x-y)(x+y)) -((x+y))/((x-y)(x+y))`

We can finally combine the fractions since they have the same denominator:
`(3x+3y - (x +y))/((x-y)(x+y))}`

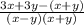
We distribute the negative:
`(3x+3y - x-y)/((x-y)(x+y))}`

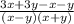
From here, we combine like terms:
`(2x+2y)/((x-y)(x+y))}`

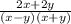
There's still one more step, we can factor out a two from the numerator:
`(2(x+y))/((x-y)(x+y))}` so that we can cancel out the term (x+y).

We are left with
`(2)/(x-y)}`