Answer:
La temperatura final del sistema es 1029,346 °C.
Step-by-step explanation:
Asumamos que el sistema conformado por el cobre y el estaño no tiene interacciones con sus alrededores. Por la Primera Ley de la Termodinámica, el cobre cede calor al estaño con tal de alcanzar el equilibrio térmico. El cobre se encuentra inicialmente en su punto de fusión, mientras que el estaño está por encima de ese punto, de modo que la transferencia de calor es esencialmente sensible:
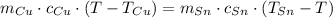
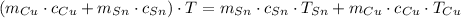
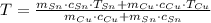 (1)
(1)
Donde:
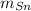 - Masa del estaño, en gramos.
- Masa del estaño, en gramos.
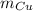 - Masa del cobre, en gramos.
- Masa del cobre, en gramos.
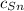 - Calor específico del estaño, en calorías por gramo-grados Celsius.
- Calor específico del estaño, en calorías por gramo-grados Celsius.
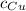 - Calor específico del cobre, en calorías por gramo-grados Celsius.
- Calor específico del cobre, en calorías por gramo-grados Celsius.
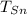 - Temperatura inicial del estaño, en grados Celsius.
- Temperatura inicial del estaño, en grados Celsius.
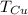 - Temperatura inicial del cobre, en grados Celsius.
- Temperatura inicial del cobre, en grados Celsius.
Si sabemos que
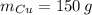 ,
,
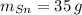 ,
,
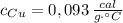 ,
,
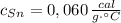 ,
,
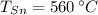 y
y
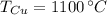 , entonces la temperatura final del sistema es:
, entonces la temperatura final del sistema es:
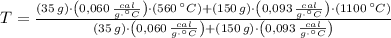
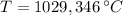
La temperatura final del sistema es 1029,346 °C.