Question

The edge of a cube was found to be 30 cm with a possible error in measurement of 0.5 cm. Use differentials to estimate the maximum possible error, relative error, and percentage error in computing the volume of the cube and the surface area of the cube. (Round your answers to four decimal places.) My Notes Ask Your Teacher

(a) the volume of the cube maximum possible error relative error percentage error cm
(b) the surface area of the cube maximum possible error relative error percentage error cm Need Help? ReadTalk to Tuter

Answer 1

Answer with Step-by-step explanation:

We are given that

Side of cube, x=30 cm

Error in measurement of edge,
`\delta x=0.5` cm

(a)

Volume of cube,
`V=x^3`

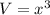
Using differential

`dV=3x^2dx`

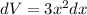
Substitute the values

`dV=3(30)^2(0.5)`

`dV=1350 cm^3`

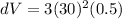
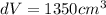
Hence, the maximum possible error in computing the volume of the cube

=
`1350 cm^3`

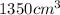
Volume of cube,
`V=(30)^3=27000 cm^3`

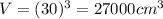
Relative error=
`(dV)/(V)=(1350)/(2700)`

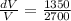
Relative error=0.05

Percentage error=
`0.05* 100=5`%

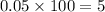Hence, relative error in computing the volume of the cube=0.05 and

percentage error in computing the volume of the cube=5%

(b)

Surface area of cube,
`A=6x^2`

`dA=12xdx`

`dA=12(30)(0.5)`

`dA=180cm^2`

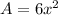
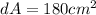
The maximum possible error in computing the volume of the cube=
`180cm^2`

`A=6(30)^2=5400cm^2`

Relative error=
`(dA)/(A)=(180)/(5400)`

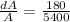
Relative error in computing the volume of the cube=0.033

The percentage error in computing the volume of the cube=
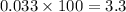`0.033* 100=3.3`%