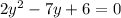Question

If α and β are the zeroes of the polynomial 6y 2 − 7y + 2, find a quadratic polynomial whose zeroes are 1 α and 1 β .

Answer 1

`2y^2-7y+6=0`

Explanation:

We are given that
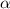`\alpha` and
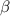`\beta` are the zeroes of the polynomial
`6y^2-7y+2`

`y^2-(7)/(6)y+(1)/(3)`

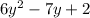
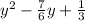
We have to find a quadratic polynomial whose zeroes are
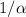`1/\alpha` and
`1/\beta`.

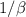General quadratic equation

`x^2-(sum\;of\;zeroes)x+ product\;of\;zeroes`

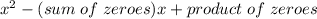
We get

`\alpha+\beta=(7)/(6)`

`\alpha \beta=(1)/(3)`

`(1)/(\alpha)+(1)/(\beta)=(\alpha+\beta)/(\alpha \beta)`

`(1)/(\alpha)+(1)/(\beta)=(7/6)/(1/3)`

`(1)/(\alpha)+(1)/(\beta)=(7)/(6)* 3=7/2`

`(1)/(\alpha)* (1)/(\beta)=(1)/(\alpha \beta)`

`(1)/(\alpha)* (1)/(\beta)=(1)/(1/3)=3`

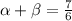
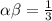
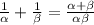
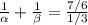
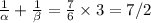
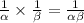
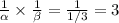
Substitute the values

`y^2-(7/2)y+3=0`

`2y^2-7y+6=0`

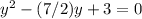
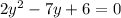
Hence, the quadratic polynomial whose zeroes are
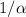`1/\alpha` and
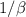`1/\beta` is given by

`2y^2-7y+6=0`