Answer:
Step-by-step explanation:
The goal here is to test whether the population proportion (p) is overstated i.e if it is actually less.
The null hypothesis & alternative hypothesis is:
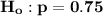
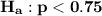
The sample proportion
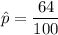

From the dot plot, we are to determine the p-value for this test i.e
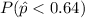
However, the number of times
 in 150 simulations = 5
in 150 simulations = 5
∴
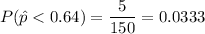
p-value = 0.033 < 0.05 < ∝
Hence, we reject the
 at 5% significance level and conclude that the proportion of shoppers who bought bananas at least once in the past month is oversrtated.
at 5% significance level and conclude that the proportion of shoppers who bought bananas at least once in the past month is oversrtated.