Question

Write the trigonometric expression in terms of sine and cosine, and then simplify.

tan θ/(sec θ − cos θ)

Answer 1

`\displaystyle (\tan\theta)/(\sec\theta - \cos\theta) = (1)/(\sin\theta) = \csc\theta`

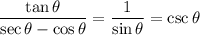
Explanation:

We have the expression:

`\displaystyle (\tan\theta)/(\sec\theta - \cos\theta)`

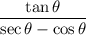
And we want to write the expression in terms of sine and cosine and simplify.

Thus, let tanθ = sinθ / cosθ and secθ = 1 / cosθ. Substitute:

`=\displaystyle ((\sin\theta)/(\cos\theta))/((1)/(\cos\theta)-\cos\theta)`

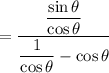
Multiply both layers by cosθ:

`=\displaystyle (\left((\sin\theta)/(\cos\theta)\right)\cdot \cos\theta)/(\left((1)/(\cos\theta)-\cos\theta\right)\cdot \cos\theta)`

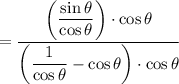
Distribute:

`\displaystyle =(\sin\theta)/(1-\cos^2\theta)`

Recall from the Pythagorean Theorem that sin²θ + cos²θ = 1. Hence, 1 - cos²θ = sin²θ. Substitute and simplify:

`\displaystyle =(\sin\theta)/(\sin^2\theta) \\ \\ =(1)/(\sin\theta)`

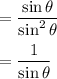
We can convert this to cosecant if we wish.