Given:
The figure of a triangle.
The perimeter of the triangle ABC is 31.
To find:
The value of x in the given triangle.
Solution:
Three sides of the triangle ABC are AB, BC, AC are their measures are
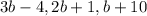 respectively.
respectively.
The perimeter of the triangle ABC is 31.

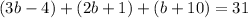
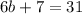
Subtract 7 from both sides.
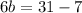

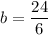

Now, the measures of the sides are:
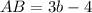
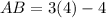
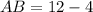
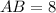
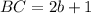
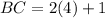

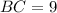
And,
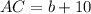
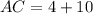
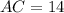
Using the law of cosines, we get
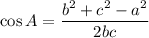
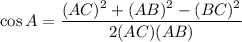
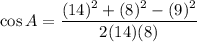
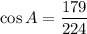
Using calculator, we get
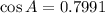
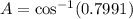
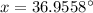
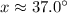
Therefore, the value of x is 37.0 degrees.