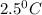Answer: The final temperature of the mixture will be
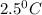
Step-by-step explanation:
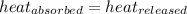
As we know that,

![m_1* c_1* (T_(final)-T_1)=-[m_2* c_2* (T_(final)-T_2)]](https://img.qammunity.org/2022/formulas/chemistry/high-school/2iwsj4v7xth00ba9r1k0icno5vnyyj4swj.png) .................(1)
.................(1)
where,
q = heat absorbed or released
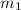 = mass of first sample of ethanol = 100 ml
= mass of first sample of ethanol = 100 ml
 = mass of second sample of ethanol = 300 ml
= mass of second sample of ethanol = 300 ml
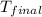 = final temperature = ?
= final temperature = ?
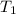 = temperature of first sample of ethanol =
= temperature of first sample of ethanol =
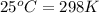
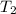 = temperature of second sample of ethanol =
= temperature of second sample of ethanol =
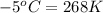
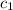 =
=
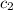 = specific heat of ethanol
= specific heat of ethanol
Now put all the given values in equation (1), we get
![-100* (T_(final)-298)=[300* (T_(final)-268)]](https://img.qammunity.org/2022/formulas/chemistry/high-school/63m7kmiq5i1jn9356cipfxhr2yo6bedwq7.png)

Therefore, the final temperature of the mixture will be