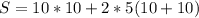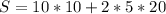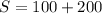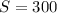Answer:
Length and Width = 10ft
Height = 5ft
Surface Area = 300 square feet
Explanation:
Given
 -- Volume
-- Volume
Let:
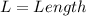
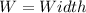

Volume (V) is calculated as:

Substitute 500 for V

Make H the subject
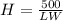
The tank has no top. So, the surface area (S) is:
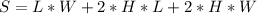

Substitute 500/LW for H
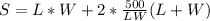
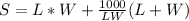
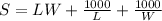
Differentiate with respect to L and to W
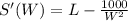
and
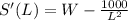
Equate both to get the critical value
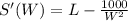 and
and
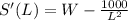
 and
and

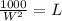 and
and
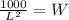
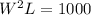 and
and
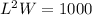
Make L the subject in
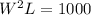
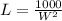
Substitute
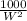 for L in
for L in
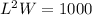
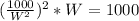
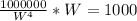

Cross Multiply
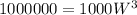
Divide both sides by 1000

Take cube roots of both sides
![\sqrt[3]{1000} = W](https://img.qammunity.org/2022/formulas/mathematics/college/xlvomvfbrtytohsu310o1mw0iu8j8i42zz.png)

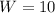
Substitute 10 for W in
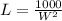
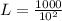

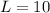
Recall that:
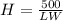
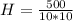
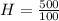
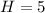
So, the dimensions are:
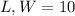 and
and
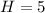
The surface area is: