Question

g In a certain underdamped RLC circuit, the voltage across the capacitor decreases in one cycle from 5.0 V to 3.8 V. The period of the oscillations is

Answer 1

The question is incomplete. The complete question is :

In a certain underdamped RLC circuit, the voltage across the capacitor decreases in one cycle from 5.0 V to 3.8 V. The period of the oscillations is 1.2 microseconds (1.2*10^-6). What is Q?

Solution :

The underdamped RLC circuit

`$v_(t) = ve^{-(R)/(2L)t} \cos \omega t$`

`$\omega = \sqrt{(1)/(LC)-(R^2)/(4L^2)}= (2 \pi)/(T)$`

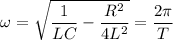
We know in one time period, v = 2v, at t = T,
`$v_t = 3.8 v$`

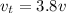
so,
`$9.8 = 5 e^{-(R)/(2L)T} \cos (2 \pi)/(T)T$`

`$e^{-(R)/(2L)T} = (3.8)/(5) * 1$`

`$(R)/(2L)T= \ln (5)/(3.8)$`

`$(R)/(L)= (2)/(1.2 * 10^(-6)) \ln (5)/(3.8)$`

`$(R)/(L) = 457.3 * 10^3$`

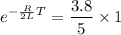
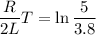
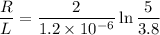
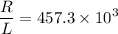
Now, Q value
`$= (1)/(R)\sqrt{(L)/(C)}$`

`$=\sqrt{(L)/(R^2C)* (L)/(L)}$`

`$=\sqrt{((L)/(R))^2 * (1)/(LC)}$`

`$(1)/(LC)=27.43 * 10^(12)$`

∴
`$Q=\sqrt{\left((1)/(457.3 * 10^3)\right)^2 * 27.43 * 10^(12)}$`

`$Q=√(131.166)$`

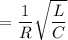
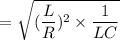
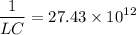
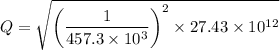
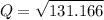
= 11.45