Question

(6) Compare a CSTR with a PFR below. a. A flow of 0.3 m3/s enters a CSTR (volume of 200 m3) with an initial concentration of species A at 200 mg/L. The reaction proceeds with 1st order kinetics and a reaction rate of 5.09 hr-1. Determine the concentration of species A leaving the reactor. (8 pts) b. If a plug flow reactor was designed to have the same efficieny as the CSTR in Part A, what would the volume of the PFR be

Answer 1

Step-by-step explanation:

Given that:

The flow rate Q = 0.3 m³/s

Volume (V) = 200 m³

Initial concentration
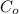`C_o` = 2.00 ms/l

reaction rate K = 5.09 hr⁻¹

Recall that:

`time (t) = (V)/(Q)`

`time (t) = (200)/(0.3)`

`time (t) = 666.66 \ sec`

`time (t) = (666.66 )/(3600) hrs`

`time (t) = 0.185 hrs`

`\text{Using First Order Reaction:}`

`(dc)/(dt)=kc`

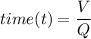
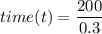
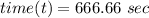
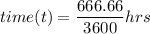
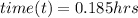
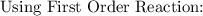
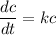
where;

`t = (1)/(k) \Big( (C_o)/(C_e)-1 \Big)`

`0.185 = (1)/(5.09) \Big ( (200)/(C_e)- 1 \Big)`

`0.942 = \Big ( (200)/(C_e)- 1 \Big)`

`1+ 0.942 = \Big ( (200)/(C_e) \Big)`

`(200)/(C_e) = 1.942`

`C_e = (200)/(1.942)`

`\mathbf{C_e = 102.98 \ mg/l}`

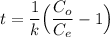
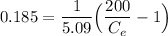
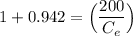
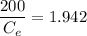
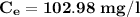
Thus; the concentration of species in the reactant = 102.98 mg/l

b). If the plug flow reactor has the same efficiency as CSTR, Then:

`t _(PFR) = (1)/(k) \Big [ In ( (C_o)/(C_e)) \Big ]`

`(V_(PFR))/(Q_(PFR)) = (1)/(k) \Big [ In ( (C_o)/(C_e)) \Big ]`

`(V_(PFR))/(Q_(PFR)) = (1)/(5.09) \Big [ In ( (200)/(102.96)) \Big ]`

`(V_(PFR))/(Q_(PFR)) =0.196 \Big [ In ( 1.942) \Big ]`

`(V_(PFR))/(Q_(PFR)) =0.196(0.663)`

`(V_(PFR))/(0.3 hrs) =0.196(0.663)`

`(V_(PFR))/(0.3*3600 sec) =0.196(0.663)`

`V_(PFR) =0.196(0.663)*0.3*3600`

`V_(PFR) = 140.34 \ m^3`

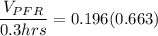
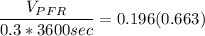
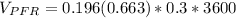
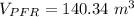
The volume of the PFR is ≅ 140 m³